Площа трикутника – повний гід з формулами та прикладами

Площа трикутника — це одна з базових тем у геометрії, яку вивчають у школі. Хоча на перший погляд вона здається простою, насправді існує багато способів знаходження площі залежно від відомих елементів фігури. У цій статті ми розберемо всі основні формули, приклади та корисні поради, щоб кожен школяр і навіть дорослий міг легко зрозуміти та застосувати знання.

Що таке площа трикутника

Площа трикутника — це величина, яка показує, яку частину площини займає дана фігура. Інакше кажучи, вона відображає розмір поверхні всередині трикутника. Площа вимірюється у квадратних одиницях, наприклад, у см², м² чи км². Цей показник має практичне значення в архітектурі, будівництві, картографії та багатьох інших сферах.

Основні способи знаходження площі трикутника

Існує декілька головних методів для того, щоб знайти площу трикутника. У кожному випадку потрібно знати певні елементи: сторони, висоту, кути або радіуси вписаного й описаного кола. Нижче наведемо найпопулярніші варіанти.

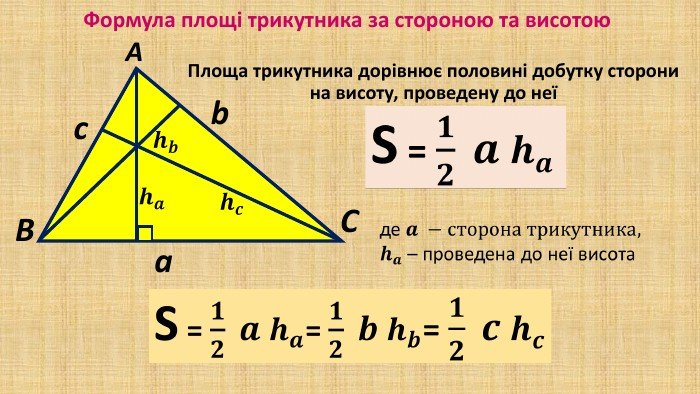
Площа трикутника через основу і висоту

Найпростіший спосіб знайти площу — це використати формулу через основу і висоту:

S = ½ · a · h

де a — довжина основи, а h — висота, проведена до цієї основи.

Цей метод дуже зручний, коли в задачі вже відома висота або її легко провести.

Площа трикутника за формулою Герона

Коли відомі всі три сторони трикутника, використовують формулу Герона:

S = √(p · (p – a) · (p – b) · (p – c))

де p — це півпериметр (p = (a + b + c) / 2), а a, b, c — сторони трикутника.

Ця формула універсальна, адже дозволяє обчислити площу без додаткових побудов.

Площа трикутника через дві сторони та кут між ними

Ще один поширений спосіб:

S = ½ · a · b · sin(γ)

де a і b — дві сторони трикутника, а γ — кут між ними.

Цей варіант часто застосовується у задачах, де відомі кути та сторони, але висота не зазначена.

Площа прямокутного трикутника

Для прямокутного трикутника формула ще простіша:

S = ½ · a · b

де a і b — катети.

Оскільки висота в цьому випадку збігається з катетом, обчислення виходять дуже легкими.

Площа трикутника через радіус вписаного кола

Якщо відомий радіус вписаного кола r і півпериметр p, тоді:

S = r · p

Ця формула часто зустрічається в олімпіадних завданнях і вищій математиці.

Площа трикутника через радіус описаного кола

Ще один цікавий варіант:

S = (a · b · c) / (4R)

де R — радіус описаного кола, а a, b, c — сторони.

Він менш поширений у школі, але дуже важливий у геометричних доказах.

Площа трикутника на координатній площині

Коли вершини трикутника задані координатами (x₁, y₁), (x₂, y₂), (x₃, y₃), використовують формулу:

S = ½ · |x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|

Цей спосіб зручний у алгебрі та аналітичній геометрії.

Приклади розв’язування задач

Приклад 1. Через основу і висоту

Основа дорівнює 10 см, висота — 6 см.
S = ½ · 10 · 6 = 30 см².

Приклад 2. За формулою Герона

Сторони трикутника: a = 7, b = 8, c = 9.
p = (7 + 8 + 9) / 2 = 12.
S = √(12 · 5 · 4 · 3) = √720 = 26,83 см².

Приклад 3. Через дві сторони і кут

a = 5, b = 6, γ = 60°.
S = ½ · 5 · 6 · sin60° = 15√3 / 2 ≈ 12,99 см².

Де застосовується площа трикутника

Знання формул для площі потрібне не лише на уроках. Наприклад:

• у будівництві для розрахунку дахів і конструкцій;
  
• у землевимірюванні при визначенні площі ділянок;
  
• у фізиці під час векторних розрахунків;
  
• у програмуванні та комп’ютерній графіці.
  

Поради для легкого запам’ятовування формул

1. Завжди визначайте, які саме елементи трикутника відомі.
   
2. Якщо є висота — використовуйте просту формулу.
   
3. Якщо відомі три сторони — найкраще підходить формула Герона.
   
4. Якщо дані кути і дві сторони — використовуйте синус.
   
5. Тренуйтеся на задачах різної складності, щоб швидко вибирати потрібний спосіб.
   

Висновок

Площа трикутника — це базова, але дуже важлива тема геометрії. Завдяки різним формулам можна знаходити площу в будь-якій ситуації: коли відомі сторони, кути, висоти або координати. Регулярна практика допоможе легко орієнтуватися в задачах і швидко знаходити рішення.

Читати далі: ГДЗ математика 5 клас Бевз – повний посібник для учнів та батьків

Часті запитання про площу трикутника